
Rumus anuitas merupakan konsep penting dalam keuangan yang digunakan untuk menghitung pembayaran berkala dalam suatu periode tertentu, seperti dalam kasus pinjaman atau investasi.
Pengertian anuitas sendiri adalah serangkaian pembayaran atau penerimaan yang sama jumlahnya dalam jangka waktu tertentu. Dengan memahami rumus anuitas, individu dan bisnis dapat mengelola keuangan dengan lebih efektif dan mencapai tujuan finansial mereka dengan lebih terencana.

Anuitas adalah angsuran dan bunga yang dibayarkan dalam jumlah yang sama dalam jangka waktu tertentu. (Credit: pexels.com)
#Pengertian Anuitas
Mengutip dari E-Modul Matematika (Peminatan): Pertumbuhan, Peluruhan, Bunga Tunggan, Bunga Majemuk, dan Anuitas, menjelaskan jika anuitas adalah sejumlah pembayaran pinjaman/hutang yang sama besarnya dan dibayarkan dalam waktu tertentu, dan terdiri atas bagian bunga dan angsuran.
Sederhananya, anuitas adalah angsuran dan bunga yang dibayarkan dalam jumlah yang sama dalam jangka waktu tertentu. Dengan rumus:
Rumus Angsuran: An = A1(1 + p)^n-1
Rumus Anuitas: AN = Mo × p ÷ [1 − (1 + p)^−n]
Selain itu, pembayaran dan penerimaan dari anuitas juga bisa berupa angsuran pinjaman, pensiun, dividen, atau bentuk lain dari arus kas yang stabil.
Baca Juga: 5 Perbedaan Hutang dan Piutang dalam Keuangan Bisnis
#Pengertian Bunga Anuitas
Sedangkan pengertian dari bunga anuitas adalah komponen dari pembayaran anuitas yang terdiri dari bunga yang harus dibayarkan atas saldo pokok yang tersisa. Dalam konteks anuitas, pembayaran berkala yang dilakukan terdiri dari dua komponen utama: bunga dan amortisasi pokok.
Bunga anuitas dihitung berdasarkan tingkat bunga yang telah ditentukan dan saldo pokok yang tersisa pada awal setiap periode pembayaran. Memastikan bahwa pemberi pinjaman atau penyedia anuitas mendapatkan kompensasi atas penggunaan uang mereka, sementara penerima anuitas secara bertahap mengurangi saldo pokok hutang mereka.
Anuitas memiliki beberapa karakteristik dasar, berikut diantaranya:
Rumus anuitas dapat digunakan dalam berbagai situasi, seperti:
Anuitas dikelompokkan menjadi 4 jenis, berikut diantaranya:
Anuitas biasa adalah jenis anuitas di mana pembayaran dilakukan pada akhir setiap periode. Jenis ini merupakan bentuk anuitas yang paling umum digunakan.
Contohnya, pembayaran angsuran KPR bulanan, penerimaan dividen saham triwulanan, penarikan dana pensiun tahunan, dan lain sebagainya.
Kemudian ada anuitas jatuh tempo, yakni anuitas yang pembayaran dilakukan pada awal setiap periode. Ini berarti pembayaran pertama dilakukan segera setelah perjanjian anuitas ditandatangani.
Contohnya, premi asuransi jiwa tahunan yang dibayarkan di awal tahun, sewa bulanan yang dibayarkan di awal bulan dan sejenisnya.
Ketiga adalah anuitas ditangguhkan, yakni jenis anuitas yang pembayaran dimulai setelah jangka waktu tertentu yang disebut periode penangguhan. Selama periode ini, investasi dapat tumbuh tanpa pembayaran.
Contohnya seperti, polis asuransi jiwa yang baru memberikan manfaat setelah 10 tahun, rencana pensiun yang baru mulai dicairkan setelah usia 60 tahun, tabungan pendidikan anak yang baru dapat digunakan setelah anak masuk perguruan tinggi dan lainnya.
Terakhir adalah anuitas langsung, yakni anuitas yang pembayarannya dimulai segera setelah investasi awal dilakukan. Biasanya digunakan oleh pensiunan yang menginvestasikan sejumlah besar uang untuk mulai menerima pembayaran pendapatan segera.
Misalnya, seseorang yang memasuki masa pensiun dapat membeli anuitas langsung dengan pembayaran lump sum sebesar Rp500.000.000 dan mulai menerima pembayaran bulanan sebesar Rp5.000.000 segera setelah pembelian dilakukan.

Ada beberapa rumus yang bisa digunakan untuk menghitung rumus anuitas ( Credit: Freepik.com)
Ada beberapa rumus anuitas yang bisa digunakan, berikut diantaranya:
Berdasarkan E-Modul Matematika (Peminatan), rumus anuitas adalah sebagai berikut:
Rumus Anuitas: AN = Mo × p ÷ [1 − (1 + p)−n]
Keterangan:
Sedangkan mengutip dari beberapa sumber lainnya, untuk rumus anuitas juga dapat dihitung dengan:
Anuitas = SP x 1 x (30/30)
Keterangan:
Dari rumus tersebut kemudian dapat dikembangkan dan disesuaikan dengan nilai dasar, menjadi:
Rumus Anuitas: P x i x[(1-i) x t) / (1+i)t-1)]
Keterangan:
Untuk anuitas biasa (pembayaran di akhir periode), rumus untuk menghitung pembayaran berkala (PMT) adalah:
PMT = (P x r) / (1 - (1+ r)^-n)
Keterangan:
Sedangkan untuk anuitas jatuh tempo (pembayaran di awal periode), rumusnya sedikit berbeda, yakni:
PMT = [(Pxr) / (1- (1+r)^-n)] x (1 +r)
Keterangan:
Perbedaan antara kedua rumus terletak pada faktor (1 + r) di akhir rumus kedua. Faktor ini memperhitungkan nilai waktu uang dan fakta bahwa pembayaran dilakukan pada awal periode dalam anuitas jatuh tempo.
Berikut beberapa contoh perhitungan anuitas
Misalnya, Budi meminjam uang sebesar Rp5.000.000 dengan bunga 12% per tahun atau 1% per bulan secara anuitas dalam 10 bulan masa pelunasan. Berapa biaya angsuran yang perlu dibayarkan budi:
Diketahui:
Penyelesaian:
AN = Mo × p ÷ [1 − (1 + p)−n] = 5000000 × 0,01 ÷ [1 − (1 + 0,01)−10] = 527.910,383
Maka bisa disimpulkan jika angsuran yang perlu dibayarkan Budi jika dibulatkan adalah Rp 528.000, berikut tabel pelunasannya:
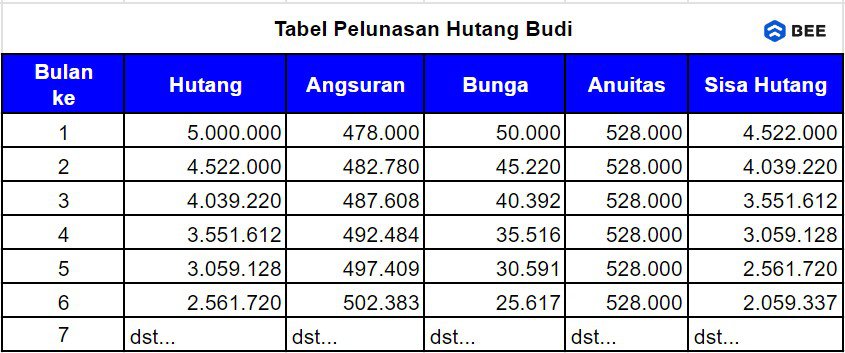
Note: contoh diambil dari E-Modul Matematika (Peminatan): Pertumbuhan, Peluruhan, Bunga Tunggal, Bunga Majemuk, dan Anuitas.
Contoh kasus, Andi seorang pemilik usaha bengkel yang meminjam modal usaha sebesar Rp 20.000.000 dengan suku bunga tahunan 12% yang harus dibayar dalam periode 1 tahun (12 bulan). Berapa bunga dan cicilannya tiap bulan?
Diketahui:
Penyelesaian:
Anuitas = P x i x[(1-i) x t) / (1+i)t-1)]
= 20.000.000 × 0,01 × [(1+0,01)^12) / (1+0,1)^12-1
= 20.000.000 x 0,01 x (1,01)^12 / (0,01)^12 -1
20.000.000 x 0,01 x 1,1268/1,1268 - 1
20.000.000 x 0,01 x 1,1268/0,1268
= 20.000.000 × 0,01 × 8,89
Hasilnya≈ 1.778.000
Sehingga, bisa disimpulkan jika cicilan dan bunga yang harus dibayar Andi sebesar Rp1.778.000
Berikut tabel bunga dan pelunasannya;
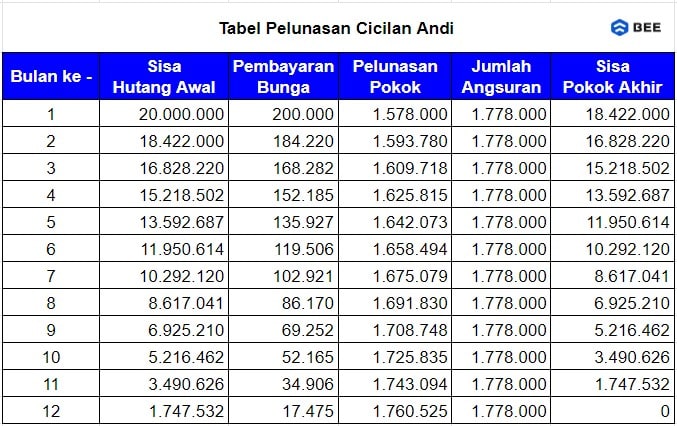
Misalkan Anda ingin membeli mobil dengan harga Rp200.000.000 dan ingin melunasinya dalam 5 tahun dengan angsuran bulanan. Suku bunga pinjaman mobil adalah 6% per tahun (0.5% per bulan). Maka, anuitasnya adalah ...
Diketahui:
Penyelesaian:
PMT = (P x r) / (1 - (1+ r)^-n)
= (200.000.000 x 0.005) / (1 - (1 + 0.005)^-60)
≈ Rp4.618.581
Maka dapat disimpulkan jika angsuran bulanan untuk melunasi pinjaman mobil Anda adalah Rp4.618.581.
Contoh kasus perhitungan anuitas jatuh tempo, misalkan Anda meminjam modal usaha sebesar Rp 15.000.000 dengan suku bunga tahunan 12% yang harus dibayar dalam periode 1 tahun (12 bulan), dan pembayaran dilakukan di awal setiap periode. Berapa anuitasnya?
Diketahui:
Penyelesaian:
PMT = [(Pxr) / (1- (1+r)^-n)] x (1 +r)
= [(15.000.000×0,01) / (1-(1+0,01)^12)] x (1+0,01)
= (15.000.000×0,01) / 1-0,8874
Maka, 15000/0,1125 ≈ 1.332.832
Kesimpulannya, Jadi, cicilan per bulannya adalah sekitar Rp 1.346.160 selama 12 bulan.
Berikut beberapa kelebihan dan kekurangan bunga anuitas:
Baca Juga: Mengenal Investasi Jangka Panjang Kunci Bisnis Berkelanjutan
Secara keseluruhan, anuitas menawarkan beberapa kelebihan. Namun, peminjam juga perlu mempertimbangkan beberapa kekurangan agar dapat membuat keputusan yang bijaksana. Semoga bermanfaat.







